期待値とは、私たちが不確実な状況で未来を予測するために役立つ概念です。確率を活用し「平均的にどのような結果が得られるか」を示す期待値は、統計学や確率論だけでなく、ビジネスや日常生活でも重要な役割を果たします。たとえば、投資におけるリスク管理やギャンブルにおける「有利・不利」の判断にも期待値は利用され、計算を通じて将来の結果を合理的に予測する指標となっています。
しかし、期待値と似た概念である「平均値」や「分散」とは異なり、期待値は単に結果の平均を意味するだけではありません。「確率で重み付けした平均」として、各結果がどのくらいの頻度で起こるかを考慮する点が特徴です。また、期待値を理解することで、私たちはより合理的な意思決定が可能になります。この記事では、期待値の基本的な定義や計算方法をわかりやすく解説し、その応用例を通じて実生活にどのように役立つかを具体的に紹介します。期待値を理解することで、未来に対する見通しを持ち、リスクや利益を適切に評価するための知識が得られるでしょう。
期待値とは?基本的な定義と意味
期待値とは、私たちが将来の結果を予測するための「平均的な見込み」を示す指標です。一般的な「平均」とは少し異なり、期待値は確率を用いて計算する点が特徴です。この考え方は、統計学や確率論で学ばれるだけでなく、ギャンブルや投資など、リスクを伴う意思決定にも深く関わっています。ここでは、期待値の基本的な定義と、その意味をわかりやすく解説していきます。
期待値とは何か?
期待値は、ある出来事が起こる確率に基づいて「平均的にどれだけの結果が得られるか」を予測するための指標です。具体的には、各結果にその発生確率を掛けて合計することで求められます。例えば、サイコロを1回振ったときの期待値は、全ての出目(1から6)が出る確率が等しいので、以下のように計算できます。
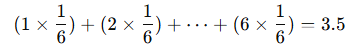
つまり、サイコロの期待値は3.5です。実際にはサイコロを振って「3.5」が出ることはありませんが、多くの回数を試行すれば、出目の平均が3.5に近づくことがわかります。この「多くの試行により収束する平均値」が期待値の概念です。
平均と期待値の違い
一見、期待値は「平均」と似たように思われがちですが、実際には異なる概念です。平均値は過去に観測された値の単純な平均を示すのに対し、期待値は「将来においてどのような結果が期待できるか」を予測する値です。特に不均等な確率を持つ場合、期待値は各結果に確率の重みをかけることで計算されるため、より精緻な予測が可能となります。例えば、不正なサイコロを使ったゲームでは、各出目の確率が異なります。この場合、期待値はその確率の重みに基づいて計算され、単純な平均とは異なる結果となります。
期待値の基本的な考え方と日常生活での応用
期待値の概念は、実は日常生活でも応用できる場面が多くあります。例えば、買い物でどのくらいの割引が期待できるか、天気予報で降水確率に基づいて傘を持つかどうか判断するなど、日々の選択や判断に期待値の考え方は密かに役立っています。こうした応用を通して、期待値は単なる数学的な概念ではなく、私たちが合理的に行動するための「道しるべ」としても機能しています。
期待値を理解することで、未来に対する予測をより正確に行えるようになり、ビジネスや投資だけでなく、日常生活においても判断力を高めることができるでしょう。
期待値の計算方法:公式と具体例
期待値の計算方法を理解することは、確率や統計の問題を解くための基礎となります。期待値は、単なる「平均」ではなく、各結果がどれだけの確率で起こるかを考慮して求める「重み付けされた平均」です。ここでは、期待値の基本的な公式と計算方法を、具体的な例を使ってわかりやすく解説します。
期待値の基本公式
期待値は、次のようにして求めます。ある出来事が発生する確率と、その出来事から得られる結果(数値)を掛け合わせ、その合計をとることで算出されます。期待値 E(X)の公式は、以下のように表されます。
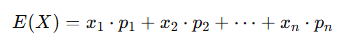
ここで、xi は各結果の値(たとえばサイコロの出目)、pi は各結果が出る確率です。
具体例1:サイコロの期待値を求める
まず、6面サイコロを振ると仮定しましょう。サイコロの各面(1〜6)は等しい確率(1/6)で出現します。この場合、サイコロの期待値は次のように計算できます。
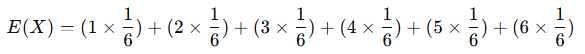
上記を計算すると、期待値 E(X)=3.5となります。つまり、サイコロを何度も振ると、出目の平均はおよそ3.5に収束することがわかります。これが期待値の基本的な考え方です
具体例2:ギャンブルでの期待値の活用
次に、ギャンブルの例を考えましょう。例えば、ゲームでコインを1回投げると仮定します。コインの表が出れば100円もらえる、裏が出れば50円払う場合、それぞれの確率は等しく1/2です。このときの期待値は以下のように計算できます。
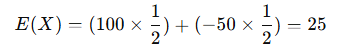
つまり、このゲームにおける期待値は25円となります。期待値がプラスであれば利益が見込め、マイナスであれば長期的に損をする可能性が高いことを示します。この例では、1回あたりの「期待値」が25円であるため、期待値を元に判断すると、このゲームはプラスの結果が見込まれると考えられます。
複雑な状況での期待値の応用
期待値の計算方法はシンプルですが、複数の要素が絡む複雑な問題でも応用可能です。例えば、投資において複数のリスクが同時に発生するようなケースでは、各シナリオの確率と利益(あるいは損失)をもとに期待値を算出し、意思決定をサポートできます。また、保険会社は、顧客ごとのリスクに基づいて期待値を計算し、どれほどの保険料を請求すべきかを決定しています。
実生活で期待値を活用するメリット
期待値を理解することは、日常の判断力を高めるためにも役立ちます。たとえば、宝くじの購入や投資の判断など、不確実な結果に対して「どのくらい得られるか」という期待値を算出すれば、合理的な意思決定が可能です。期待値は未来の予測に役立つ指標であり、リスクと利益を比較して判断する基盤として利用されています。
期待値を活用することで、私たちは長期的な展望を持った判断ができるようになり、ビジネスや個人の意思決定にも役立つスキルとなるでしょう。
期待値の性質と応用:ビジネスや統計分析での活用
期待値は、ビジネスや統計分析で将来の結果を予測するための強力なツールです。確率に基づいて「平均的な見込み」を示す期待値は、ただの計算値にとどまらず、長期的な意思決定やリスク評価を支える重要な指標となります。ここでは、期待値の基本的な性質と、それがどのようにビジネスや統計分野で応用されているのかを見ていきましょう。
期待値の基本的な性質
期待値には、特にビジネスや統計分析において重要ないくつかの性質があります。代表的な性質として以下の2つが挙げられます。
1.加法性
複数の独立したイベントの期待値の和は、各イベントの期待値を足し合わせることで求められます。つまり、期待値 E(X+Y)=E(X)+E(Y) です。この性質により、ビジネスにおける複数プロジェクトの収益期待値を個別に計算し、合計して全体の収益見込みを出すことができます
2.スケーリング
期待値は定数倍の影響をそのまま受けます。例えば、あるプロジェクトの期待収益が2倍になると仮定した場合、期待値も2倍になります。これは、期待値の計算が確率に基づく「重み付けされた平均」であることからくる性質です。このスケーリングの性質は、ビジネスの予算や資金計画でリターンを増減させた場合の影響を簡単に把握するのに役立ちます。
ビジネスでの期待値の応用例
期待値は、ビジネスの意思決定において重要な役割を果たします。以下は、期待値が具体的にどのように活用されているかを示す例です。
1.投資リターンの予測
投資の際に、期待されるリターンを基にリスクとリターンを評価し、合理的な判断を下します。たとえば、ある投資が50%の確率で10万円の利益を生み出し、50%の確率で5万円の損失をもたらす場合、その投資の期待値は (10 万×0.5)+(−5 万×0.5)=2.5 万円 となり、長期的には利益が見込まれると判断できます。この期待値を基に、リスクを取るべきか、保守的な選択をするべきかを検討することができます。
2.保険におけるリスク管理
保険会社は、事故や災害の発生確率と支払額から期待値を計算し、保険料を設定します。期待値が高いリスクについては保険料を上げる、あるいは契約条件を調整することで収支のバランスを保っています。このように、期待値を用いてリスクを数値化し、適切な料金設定を行うことで、保険会社は持続的な収益を確保しています。
3.マーケティングキャンペーンの効果予測
マーケティングキャンペーンにおいても、期待値は費用対効果を予測するためのツールとして活用されています。例えば、キャンペーンに1,000人が参加し、そのうち30%が製品を購入する見込みで、購入者1人あたりの利益が500円の場合、期待される収益は 1000×0.3×500=15 万円 です。この期待値により、キャンペーン費用との比較が可能になり、実施の是非を判断できます
統計分析での期待値の活用
統計分析においても、期待値はデータの中心傾向を示す指標として使われます。例えば、アンケート調査などのデータを分析する際、全体の期待値を求めることで「平均的な結果」が把握できます。また、データの分散や標準偏差と組み合わせることで、データのばらつきや偏りも確認でき、データの理解が深まります。
期待値は、確率をもとに「将来的にどれだけの成果が見込めるか」を示す重要な指標です。ビジネスでは、期待値を活用してリスクを管理し、より合理的な意思決定を行います。また、統計分析においても、期待値はデータの中心的な傾向を示すための基礎として不可欠な概念です。期待値を理解し活用することで、将来の見通しを立てやすくなり、様々な分野で有用な判断材料を得られるでしょう。
期待値がもたらす合理的な意思決定
期待値は、不確実な未来を予測するための重要な指標であり、ビジネスや日常生活においてリスクとリターンを評価するために不可欠なツールです。確率を考慮した「重み付けされた平均」として、期待値は、ギャンブルや投資でのリスク管理、マーケティングキャンペーンの費用対効果、保険業界での料金設定など、さまざまな場面で役立ちます。
また、期待値の性質である「加法性」や「スケーリング」によって、複数のリスクや利益を組み合わせた予測もシンプルに行うことが可能です。統計分析の場面では、データの中心傾向を理解し、偏りやばらつきを評価するための基礎としても使用され、データ全体の理解を助けます。
期待値を理解し、活用することで、私たちは未来のリスクを計画的に管理し、より合理的な意思決定を行うことができます。不確実な未来を前にして、期待値というツールは、リスクとリターンを冷静に見極め、より効果的な選択をサポートしてくれるでしょう。




コメント